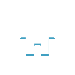的天气、地形、武器等一系列因素参数，那么一个人战力的高低y，就取决于x1，x2，μ这三个变量。

    假设现在有甲、乙两人，甲主练剑法，乙主练内功，可得x甲1＞x乙1，x甲2＜x乙2，关键的问题就在于当μ相同的情况下，此时y甲和y乙孰大孰小？

    此时根据石破天、张无忌、虚竹等人的例子可以得知，当x2位于一个极大值时，无论x1取何值，y都无比大，即内力水平无比高时，战斗力水平都会十分夸张。

    由此可见，当x2到达一个极大的区间时，x1和μ对y的相关系数都会变弱。那么问题就又变成了x2的极大区间在哪里，练内功之人如何使自己的x2到达这个区间。

    无论剑法武功还是内功水平，都是需要时间去修炼的，修炼的时间越长，水平自然越高，那么可以认为x1和x2是一个关于时间的单调递增函数，设一个人的生命总长为定值t，那么由此可得：x1=f（a，t1），x2=f（b，t2），t1t2=t。

    其中a表示影响练剑进度的参数向量，包括悟性、资质等参数变量，b则表示影响内功进度的参数向量，包括内功等级、根骨天赋等变量，因此，x1和x2并非线性函数。

    同时由于北冥神功、吸功大法、灌顶这样的内功存在，使得x2甚至可以不是时间t的函数，从而成为阶梯函数，但是这样可能会导致功力不纯，战斗过程中出现控制失灵等问题，y不能完全认为是x2的单调增函数。

    同时再根据风清扬的叙述，参数变量悟性p在x1中相关系数极大，在p≥λ时，λ为某一个特殊值，x1会无穷大，从而使得y无穷大，大到足以忽略x2的影响，例如越女阿青，独孤求败，燕十三的夺命十五剑和剑圣的剑二十三。

    按理来说，越女阿青、独孤求败等人的y值≥石破天、虚竹等人的y值，那么也就意味着x1比x2对y的影响力更强。

    但是由于p≥λ的条件太过苛刻，古往今来很少有人达到，所以出现这一事件的概率非常小，故而可得出结论：当p≥λ时，更适合练剑，而当p＜λ时，花时间修炼内功更容易使y取极大值。笔趣阁读书免费小说阅读_www.biqugedu.com

『加入书签，方便阅读』